
贝叶斯定理学习
看到一篇很好的文章,值得记录。转载自贝叶斯定理简介。
一、什么是贝叶斯推断
贝叶斯推断(Bayesian inference)是一种统计学方法,用来估计统计量的某种性质。 它是贝叶斯定理(Bayes’ theorem)的应用。英国数学家托马斯·贝叶斯(Thomas Bayes)在1763年发表的一篇论文中,首先提出了这个定理。 贝叶斯推断与其他统计学推断方法截然不同。它建立在主观判断的基础上,也就是说,你可以不需要客观证据,先估计一个值,然后根据实际结果不断修正。正是因为它的主观性太强,曾经遭到许多统计学家的诟病。 贝叶斯推断需要大量的计算,因此历史上很长一段时间,无法得到广泛应用。只有计算机诞生以后,它才获得真正的重视。人们发现,许多统计量是无法事先进行客观判断的,而互联网时代出现的大型数据集,再加上高速运算能力,为验证这些统计量提供了方便,也为应用贝叶斯推断创造了条件,它的威力正在日益显现。
二、贝叶斯定理
要理解贝叶斯推断,必须先理解贝叶斯定理。后者实际上就是计算”条件概率”的公式。
所谓”条件概率”(Conditional probability),就是指在事件B发生的情况下,事件A发生的概率,用P(A|B)来表示。
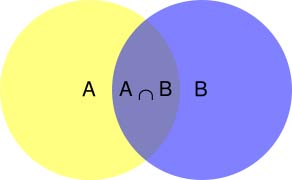 根据文氏图,可以很清楚地看到在事件B发生的情况下,事件A发生的概率就是P(A∩B)除以P(B)。
根据文氏图,可以很清楚地看到在事件B发生的情况下,事件A发生的概率就是P(A∩B)除以P(B)。
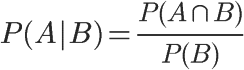 因此,
因此,
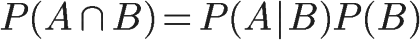 同理可得,
同理可得,
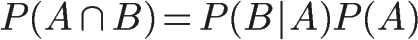 所以,
所以,
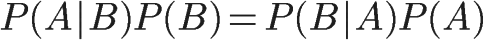 即
即
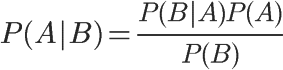 这就是条件概率的计算公式。
这就是条件概率的计算公式。
三、全概率公式
由于后面要用到,所以除了条件概率以外,这里还要推导全概率公式。
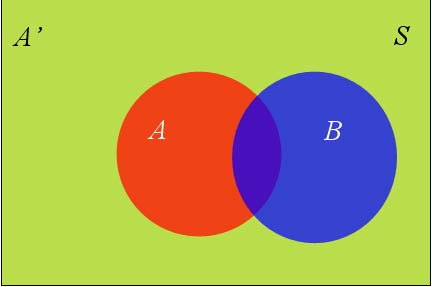
假定样本空间S,是两个事件A与A’的和。
 上图中,红色部分是事件A,绿色部分是事件A’,它们共同构成了样本空间S。
在这种情况下,事件B可以划分成两个部分。
上图中,红色部分是事件A,绿色部分是事件A’,它们共同构成了样本空间S。
在这种情况下,事件B可以划分成两个部分。
 即
即
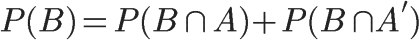 在二中推导,已知
在二中推导,已知
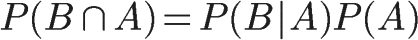 所以
所以
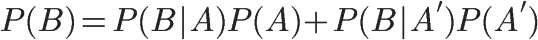 这就是全概率公式。它的含义是,如果A和A’构成样本空间的一个划分,那么事件B的概率,就等于A和A’的概率分别乘以B对这两个事件的条件概率之和。
这就是全概率公式。它的含义是,如果A和A’构成样本空间的一个划分,那么事件B的概率,就等于A和A’的概率分别乘以B对这两个事件的条件概率之和。
将这个公式代入上一节的条件概率公式,就得到了条件概率的另一种写法
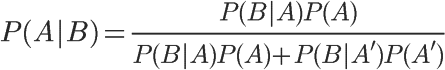
四、贝叶斯推断的含义
对条件概率公式进行变形,可以得到如下形式:
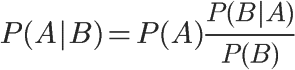 我们把P(A)称为”先验概率”(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。P(A|B)称为”后验概率”(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。P(B|A)/P(B)称为”可能性函数”(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。
我们把P(A)称为”先验概率”(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。P(A|B)称为”后验概率”(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。P(B|A)/P(B)称为”可能性函数”(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。
所以,条件概率可以理解成下面的式子:
后验概率 = 先验概率 x 调整因子
这就是贝叶斯推断的含义。我们先预估一个”先验概率”,然后加入实验结果,看这个实验到底是增强还是削弱了”先验概率”,由此得到更接近事实的”后验概率”。
| 在这里,如果”可能性函数”P(B | A)/P(B)>1,意味着”先验概率”被增强,事件A的发生的可能性变大;如果”可能性函数”=1,意味着B事件无助于判断事件A的可能性;如果”可能性函数”<1,意味着”先验概率”被削弱,事件A的可能性变小。 |
五、【例子】水果糖问题
为了加深对贝叶斯推断的理解,我们看两个例子。

第一个例子。两个一模一样的碗,一号碗有30颗水果糖和10颗巧克力糖,二号碗有水果糖和巧克力糖各20颗。现在随机选择一个碗,从中摸出一颗糖,发现是水果糖。请问这颗水果糖来自一号碗的概率有多大?
我们假定,H1表示一号碗,H2表示二号碗。由于这两个碗是一样的,所以P(H1)=P(H2),也就是说,在取出水果糖之前,这两个碗被选中的概率相同。因此,P(H1)=0.5,我们把这个概率就叫做”先验概率”,即没有做实验之前,来自一号碗的概率是0.5。
| 再假定,E表示水果糖,所以问题就变成了在已知E的情况下,来自一号碗的概率有多大,即求P(H1 | E)。我们把这个概率叫做”后验概率”,即在E事件发生之后,对P(H1)的修正。 |
根据条件概率公式,得到
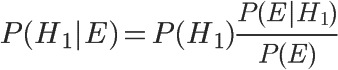
| 已知,P(H1)等于0.5,P(E | H1)为一号碗中取出水果糖的概率,等于0.75,那么求出P(E)就可以得到答案。根据全概率公式, |
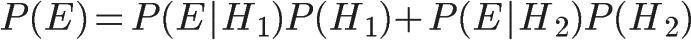
所以,
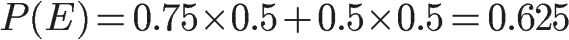 将数字代入原方程,得到
将数字代入原方程,得到
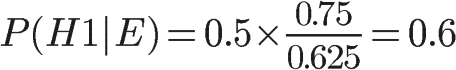 这表明,来自一号碗的概率是0.6。也就是说,取出水果糖之后,H1事件的可能性得到了增强。
这表明,来自一号碗的概率是0.6。也就是说,取出水果糖之后,H1事件的可能性得到了增强。
六、【例子】假阳性问题
第二个例子是一个医学的常见问题,与现实生活关系紧密。
已知某种疾病的发病率是0.001,即1000人中会有1个人得病。现有一种试剂可以检验患者是否得病,它的准确率是0.99,即在患者确实得病的情况下,它有99%的可能呈现阳性。它的误报率是5%,即在患者没有得病的情况下,它有5%的可能呈现阳性。现有一个病人的检验结果为阳性,请问他确实得病的可能性有多大?
假定A事件表示得病,那么P(A)为0.001。这就是”先验概率”,即没有做试验之前,我们预计的发病率。再假定B事件表示阳性,那么要计算的就是P(A|B)。这就是”后验概率”,即做了试验以后,对发病率的估计。
根据条件概率公式,
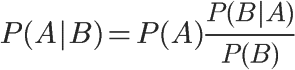 用全概率公式改写分母,
用全概率公式改写分母,
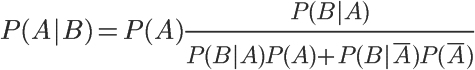 将数字代入,
将数字代入,
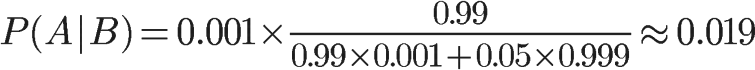 我们得到了一个惊人的结果,P(A|B)约等于0.019。也就是说,即使检验呈现阳性,病人得病的概率,也只是从0.1%增加到了2%左右。这就是所谓的”假阳性”,即阳性结果完全不足以说明病人得病。
我们得到了一个惊人的结果,P(A|B)约等于0.019。也就是说,即使检验呈现阳性,病人得病的概率,也只是从0.1%增加到了2%左右。这就是所谓的”假阳性”,即阳性结果完全不足以说明病人得病。
为什么会这样?为什么这种检验的准确率高达99%,但是可信度却不到2%?答案是与它的误报率太高有关。
Let me know what you think of this article on twitter @Yanlei_Hello or leave a comment below!