
Poisson分布
1 minute read
一、Poisson分布
Poisson分布,翻译为泊松分布。由二项分布演进而来。二项分布十分好理解,给你n次机会抛硬币,硬币正面向上的概率为p,问在这n次机会中有k次(k<=n)硬币朝上的概率为多少?
Poisson分布公式为:
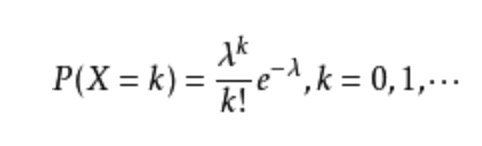 泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生率。 泊松分布适合于描述单位时间内随机事件发生的次数。泊松分布的期望和方差均为λ。
泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生率。 泊松分布适合于描述单位时间内随机事件发生的次数。泊松分布的期望和方差均为λ。
说明两点:
-
泊松分布是离散型概率分布,表示(固定尺度的)连续区间(如时间,距离)上给定的事件发生次数的概率,所以可以看做泊松分布中n是无穷大的。二项分布是固定实验次数下,事件发生次数的概率,n是有界的。
-
泊松分布中发生次数的期望是固定的 λ,事件发生的概率p不定,p=λ//n;二项分布中事件发生的概率p是固定的,发生次数的期望不定,λ=n*p。
二、泊松分布与二项分布
泊松分布是从二项分布而来的,在二项分布的伯努力试验中,如果试验次数n很大,二项分布的概率p很小,且乘积λ= n p比较适中,则事件出现的次数的概率可以用泊松分布来逼近。
三、由二项分布推导泊松分布
首先,e的定义:
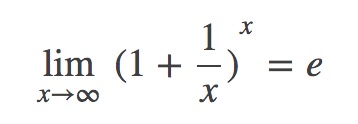 二项分布公式:
二项分布公式:
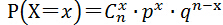 推导如下:
推导如下:
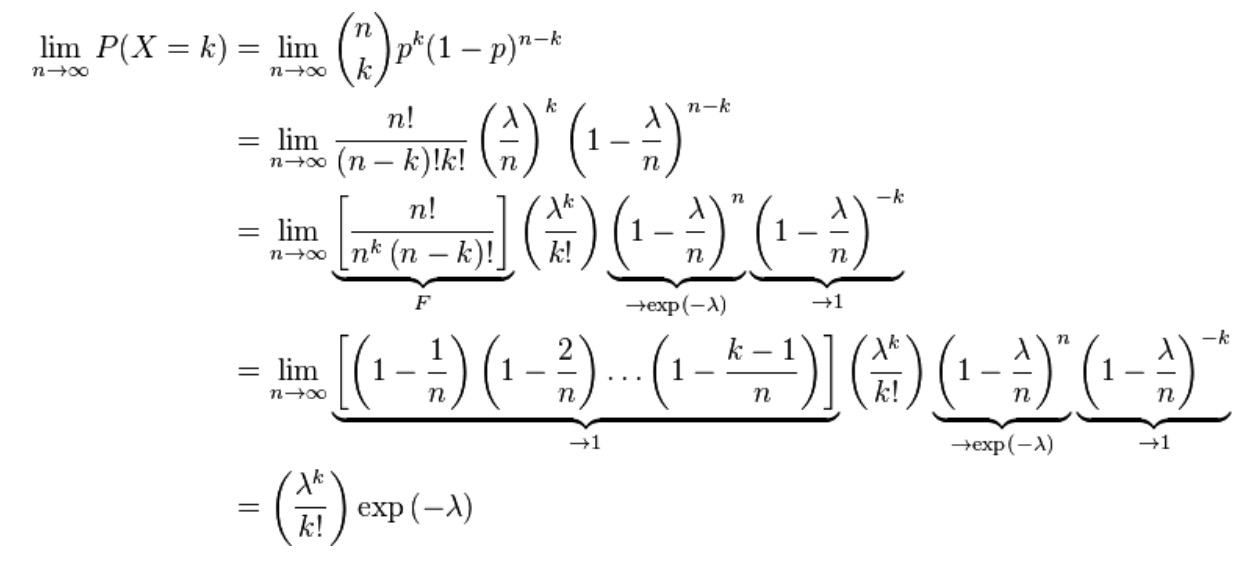
I feedback.
Let me know what you think of this article on twitter @Yanlei_Hello or leave a comment below!
Let me know what you think of this article on twitter @Yanlei_Hello or leave a comment below!
comments powered by Disqus